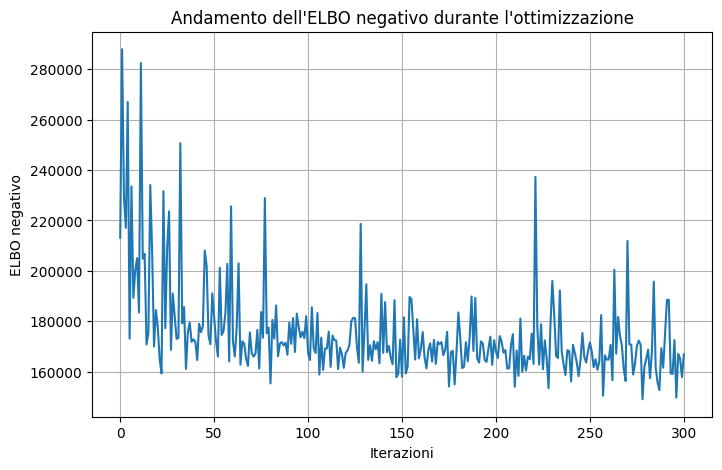
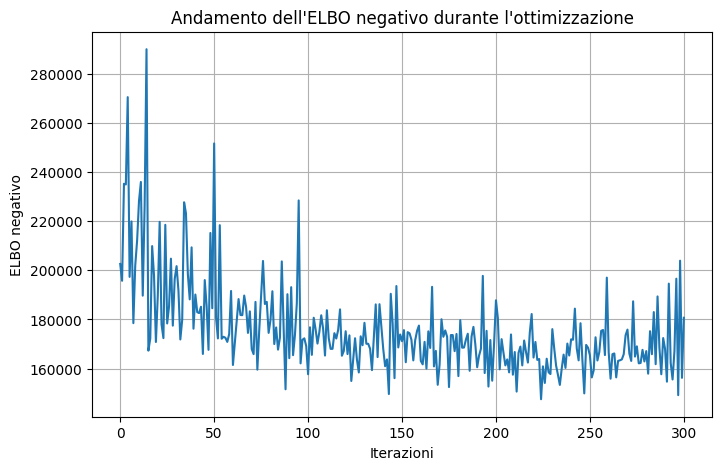
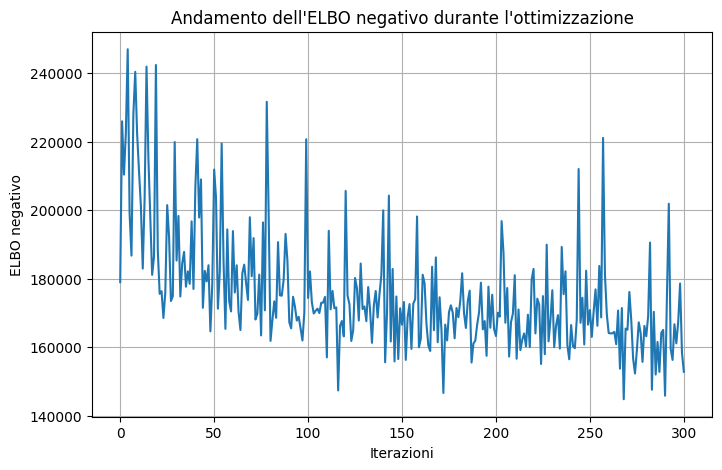
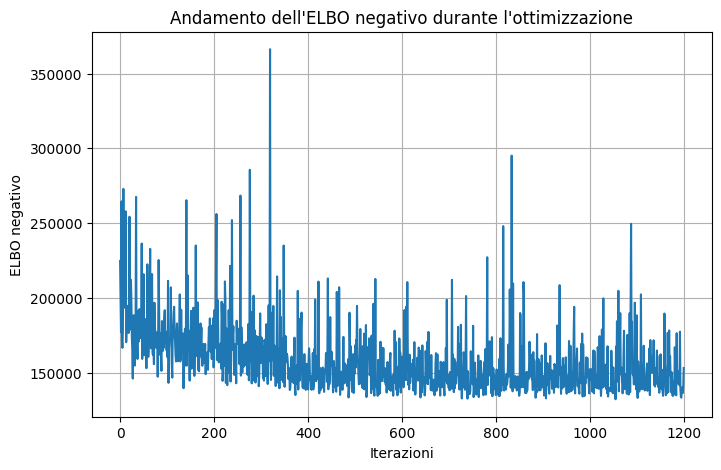
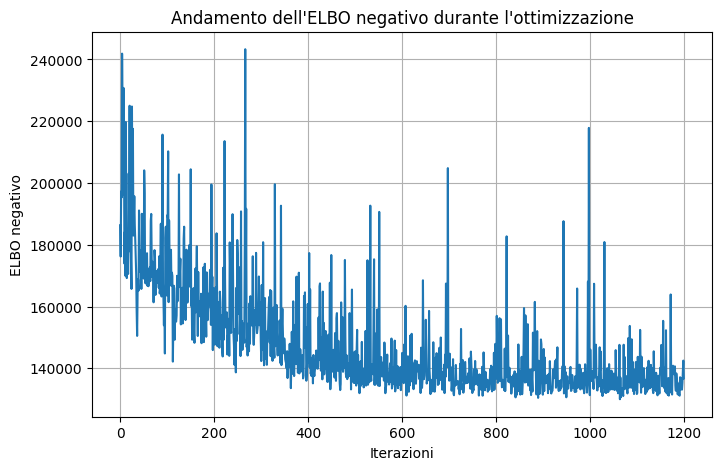
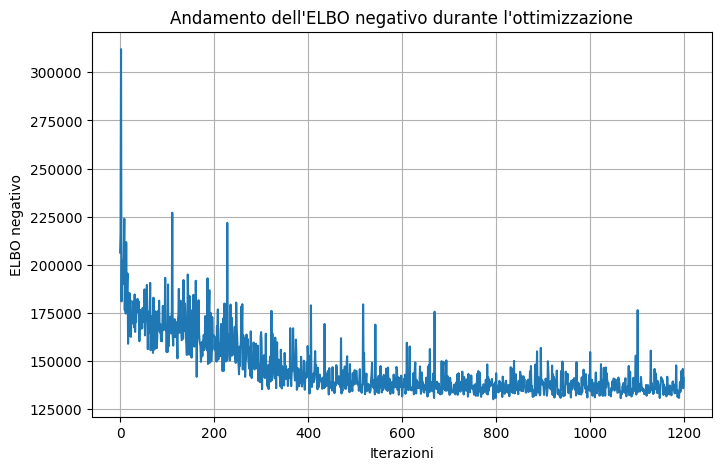
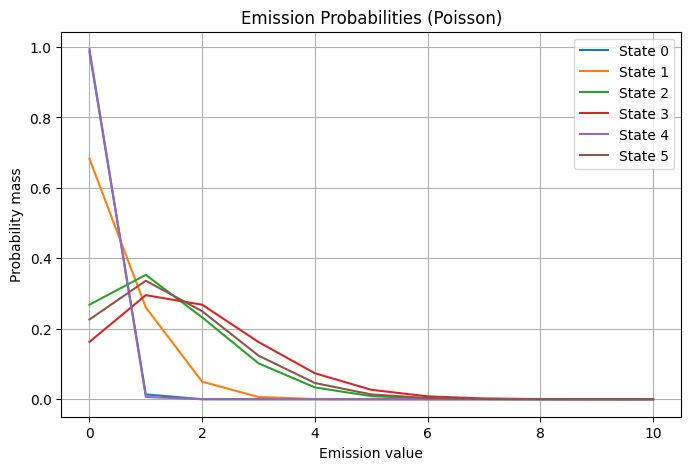
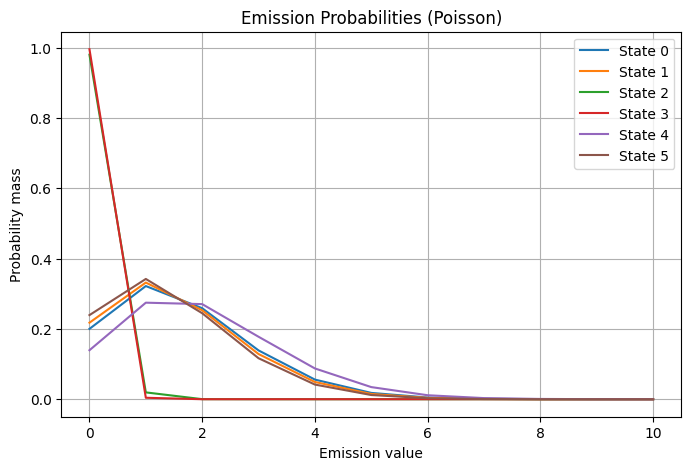
Code
import pandas as pd
import numpy as np
from hmmlearn import hmm
import matplotlib.pyplot as plt
from pyprojroot import here
import pyro
import pyro.distributions as dist
import pyro.distributions.constraints as constraints
from pyro.infer import SVI, TraceEnum_ELBO
from pyro.optim import Adam
from scipy.stats import poisson
import torch
import seaborn as sns
import collections
data = pd.read_csv(here("data/recent_donations.csv"))
data
# remove columns y_2020 to y_2023
# data = data.drop(columns=["y_2020", "y_2021", "y_2022", "y_2023"])| unique_number | class_year | birth_year | first_donation_year | gender | y_2009 | y_2010 | y_2011 | y_2012 | y_2013 | y_2014 | y_2015 | y_2016 | y_2018 | y_2019 | y_2017 | y_2020 | y_2021 | y_2022 | y_2023 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 26308560 | (1960,1970] | 1965 | 1985 | M | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 3 | 1 |
| 1 | 26309283 | (1960,1970] | 1966 | 2002 | M | 2 | 1 | 2 | 2 | 1 | 1 | 3 | 3 | 4 | 1 | 3 | 3 | 3 | 3 | 4 |
| 2 | 26317365 | (1960,1970] | 1961 | 1984 | M | 4 | 2 | 3 | 3 | 3 | 4 | 3 | 3 | 2 | 3 | 3 | 2 | 0 | 1 | 0 |
| 3 | 26318451 | (1960,1970] | 1967 | 1989 | M | 0 | 3 | 3 | 4 | 4 | 4 | 2 | 3 | 3 | 1 | 2 | 3 | 1 | 0 | 0 |
| 4 | 26319465 | (1960,1970] | 1964 | 1994 | F | 1 | 2 | 2 | 1 | 2 | 1 | 1 | 0 | 0 | 2 | 1 | 1 | 1 | 1 | 1 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 9231 | 27220599 | (1970,1980] | 1980 | 2022 | M | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 |
| 9232 | 27220806 | (2000,2010] | 2002 | 2022 | M | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 3 |
| 9233 | 27221247 | (1990,2000] | 2000 | 2022 | F | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 |
| 9234 | 27221274 | (1960,1970] | 1966 | 2022 | F | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 3 |
| 9235 | 27221775 | (2000,2010] | 2004 | 2022 | M | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 1 |
9236 rows × 20 columns